Классификация методом максимальной энтропии

Наивный байесовский классификатор, о котором я уже писал, один из самых простых классификационных алгоритмов. В этой заметке я опишу более сложный алгоритм — метод максимальной энтропии, который, в ряде случаев, может оказаться существенно более точным. К своему удивлению, я не нашел в рунете более менее полного описания этого алгоритма классификации. Поэтому, считаю полезным поделиться этими знаниями.

Как и в предыдущем случае, описание разбито на две части: теорию и практику. В теоретической части описываются вопросы связанные с математической моделью классификатора. В практической части, содержится описание, как максимально быстро получить работающий классификатор для практических нужд на Java. Исходный код работающего примера доступен на github.

Мотивация к использованию Link to heading

У байеса есть несомненные преимущества: он эффективен в обучении, может использовать параллелизм современного железа. Но есть у него и минусы. Именно они могут побудить вас использовать более сложные алгоритмы. Таких минусов несколько:

одна из систематических ошибок байеса связана с предположением условной независимости классификационных признаков (слов, в случае классификации документов). На практике, это предположение часто оказывается ложным. Например, пара слов “курильский” и “бобтейл” гораздо чаще встречается вместе, чем “бобтейл” и “турбонаддув” или “курильский” и “кальян”. Не учитывая эту информацию, байесовский классификатор имеет тенденцию отклонения в сторону классов с высоким уровнем зависимости между словами (так называемая, проблема evidence double-counting’а).
вероятностные оценки, которые дает байес могут быть сильно искажены для редких документов (подробнее об этом ниже).

Метод максимальной энтропии очень тесно связан с другим распространенным алгоритмом машинного обучения, – логистической регрессией. Люди, знакомые с логистической или линейной регрессией, найдут много знакомого в этом описании.

Теоретические основы Link to heading

Байесовский классификатор оперирует на основании таблицы весов, которые он получает на этапе обучения из частотности классификационных признаков в пределах классов, – по одному параметру на каждую пару классификационный признак+класс. То есть, всего таких весов n*k, где n–количество классов, а k–количество классификационных признаков.

На этапе классификации maxent очень похож на байесовский классификатор. Он основывается на такой же таблице весов и экспоненциальной модели классификации, которая используется в байесе для формирования вероятностного пространства из логарифмических оценок.

Для дальнейшего повествования введем следующую нотацию. Допустим, у нас есть n классов c₁, c₂,…, c_n, и k классификационных признаков: F^I,F^II,…,F^k. ) Классификационный признак – это бинарная функция над документом. Например:

F = function(d) { d.contains("бухгалтерия") }

На основании классификационных признаков генерируются классификационные индикаторы f₁, f₂,…, f_k*n, по одному индикатору на каждую пару признак+класс. Классификационный индикатор – это булева функция над парой документ+класс. Она истинна только когда истинен соответствующий классификационный признак и совпадает переданный класс.

	C₁	C₂
F^I	f₁	f₂
F^II	f₃	f₄
F^III	f₅	f₆

Взаимосвязь классов, классификационных признаков и индикаторов

Пример классификационного индикатора:

f = function(c, d) { с == "SPAM" && F(d) }

Обратите внимание, классификационные индикаторы нумеруются по сквозному принципу. Индикаторы, дающие единицу как остаток от деления на количество классов, срабатывают (возвращают истину) только на первый класс, кратные двойке на второй и т.д. Такой подход не является обязательным при реализации классификатора, но для осознания теории важно понимать разницу между признаком и индикатором, а также разницей в их нумерации.

Непосредственно классификация происходит по формуле:

$$P(c\mid d,\lambda)=\frac {\exp\sum_i^{n \times k}{\lambda_i}f_i\left(c,d\right )} {\sum_{\tilde{c}\in C}{\exp\sum_i^{n \times k}{\lambda_i}f_i\left(\tilde{c},d\right )}}$$

Классификационная формула метода максимальной энтропии (Формула №1)

В этой формуле:

$ f_i $ — i-ый классификационный индикатор (значение 0 или 1);
$ \lambda_i $ — вес i-го классификационного индикатора $ f_i $;
$ c $ — класс-гипотеза;
$ C $ — множество всех возможных классов;
$ d $ — классифицируемый документ.

У каждого индикатора $ f_i $ есть свой вес $ \lambda_i $, который описывает взаимосвязь между соответствующим классификационным признаком и классом. Чем больше вес, тем сильнее связь. Таким образом, числитель дроби описывает экспоненту весов для класса-гипотезы, а знаменатель нормирует значение по единице. Самое сложная часть этой формулы – набор весов $ \lambda $, который приходится путем численной оптимизации, о которой мы поговорим позже.

Результатом этого отношения является не просто классификационное решение, а значение вероятности для заданного класса. Один из плюсов maxent-классификации заключается в том, что она гораздо более точно моделирует вероятностное распределение классов.

На этом сходства заканчиваются и начинаются различия. Maxent-классификатор имеет несколько существенных отличий от байесовского:

он является conditional, а не joint-классификатором;
он основывается на взаимосвязи энтропии вероятностного распределения и его равномерности;
он использует итеративные алгоритмы подбора параметров модели, которые сложнее в реализации и более ресурсоемкие.

Все три различия необходимо рассмотреть более подробно.

Joint vs. Conditional-модели Link to heading

Байес для классификации использует следующую формулу: P(d|c)P(c), что является совместным распределением (joint distribution) документов и классов: P(d∩c). В отличии от байеса, классификатор максимальной энтропии моделирует распредение P(c|d) напрямую, используя обучающую выборку для подбора оптимальных параметром распределения. Есть две причины, по которым этот подход может быть предпочтителен.

Во-первых, joint-классификаторы игнорируют вероятность документа как такового. Это правомерно, если вы хотите получить только классификацию, но не вероятностное распределение классов.

Note

Классификацией называется список классов отсортированный по убыванию их вероятностей. При этом, вы не знаете их численные значения, только порядок. Классификации, впрочем, достаточно для большинства прикладных задач.

Вероятностные оценки восстанавливаемые из логарифмических оценок байеса являются апроксимацией. Причем, чем меньше априорная вероятность документа, тем сильнее будет искажена восстановленная оценка.

Во-вторых, conditional-модели позволяют более адекватно моделировать зависимости между словами. Представьте, обучающую выборку из следующих двух документов:

class   text
-----------------------
USA     San Francisco
China   Beijing

Для такого корпуса будут построена следующие таблицы весов:

        Naïve Bayes                    MaxEnt
                USA  China                  USA  China
--------------------------    ------------------------
San          -0.847 -1.609    San         0.639 -0.859
Francisco    -0.847 -1.609    Francisco   0.639 -0.859
Beijing      -1.946 -0.511    Beijing    -2.234  0.762
--------------------------    ------------------------
Total        -3.640 -3.729    Total      -0.956 -0.956

Обратите внимание, что у байеса сумма столбцов по двум классам не равна. Оценка в пределах класса USA немного выше. Поэтому, если вы попытаетесь классифицировать документ “San Francisco Beijing”, он попадет в класс USA. Так происходит из-за высокой зависимости слов “San” и “Francisco”. Байес считает их дважды. По этой причине документ и попадает в класс USA.

Maxent-классификатор способен определить такого рода зависимость между классификационными признаками и демпировать их вес, чтобы избежать проблемы double-counting’а. В этом случае, он корректно определит вероятность классов как 50/50%.

Принцип максимальной энтропии Link to heading

Информационная энтропия — это мера неопределенности вероятностного распределения.

$$H(X)=-\sum_{x\in\Omega}P(x)\log P(x)$$

Формула расчета энтропии для дискретного вероятностного распределения

В бытовом понимании, энтропия говорит о том, насколько тяжело делать предсказания о событиях описываемых вероятностным распределением. Чем больше энтропия, тем тяжелее делать предсказания.

На первый взгляд может показаться, что энтропию надо минимизировать. Давайте разберем небольшой пример, показывающий почему это не так.

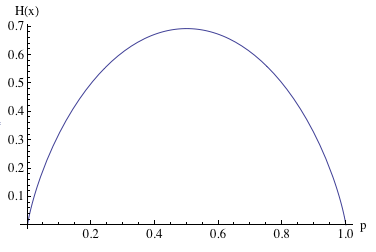
Энтропия произвольной монеты — График энтропии для монеты с произвольным значением P(H)

На этом графике показана энтропия распределения Бернулли в зависимости от его единственного параметра. Это распределение описывает процесс кидания монетки с заданной вероятностью выпадения орла или решки. Обратите внимание, в точках 0 и 1 энтропия равна нулю. Нет никакой неопределенности, всегда выпадает одна и та же сторона монеты. Максимальна же энтропия в точке 0.5, когда выпадение орла и решки равновероятно. Этот пример иллюстрирует одну важную особенность энтропии, чем больше энтропия распределения, тем распределение более равномерно.

Равномерность распределения – очень полезное качество в задачах классификации. Из всех распределений соответствующих эмпирическим данным, следует выбирать распределение обладающее наибольшей равномерностью (и, как следствие, наибольшей энтропией). В противном случае, вы выбираете распределение которое содержит информацию, подтверждения которой нет в обучающем корпусе документов. Именно поэтому maxent-классификатор максимизирует энтропию.

Проиллюстрируем это на примере. Допустим, вы кидаете монету три раза и все три раза она падает орлом вверх. Существуют ли объективные причины подозревать монету в нечестности (P(H)≠P(T))? С наивной точки зрения, вероятность выпадения орла составляет 100%, что является экстремумом нечестности. Но трех бросков определенно недостаточно, чтобы статистическая вероятность события была репрезентативна в отношении истинной вероятности. В статистике эта проблема решается при помощи доверительных интервалов.

Note

Доверительный интервал – это интервал оцениваемого параметра, такой, что в него попадает истинное значение параметра с заданной вероятностью, которую называют уровень доверия. Если не указано явно, подразумевается, что доверительный интервал обладает уровнем доверия 0.95.

Если мы посчитаем доверительный интервал вероятности выпадения решки (здесь я для расчета использую доверительный интервал Вильсона), то он составит: 0-79%, 0-66% и 0-56% для первого, второго и третьего броска соответственно. Даже после третьего броска диапазон истинной вероятности довольно широкий.

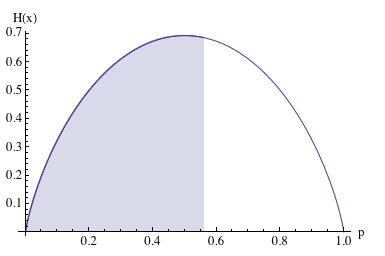
Энтропия произвольной монеты после третьего броска — Доверительный интервал после трех бросков монеты

Так какую вероятность нам выбрать для моделирования такой монеты, если результаты 3-х бросков всё что у нас есть? Принцип максимальной энтропии говорит – 0.5. Мы не получили достаточно информации, чтобы утверждать, что целевое распределение не равномерно. А пока таковой нет, мы должны отталкиваться от предположения равномерности истинного распределения.

Выбор параметров модели Link to heading

Последний вопрос, который требует обсуждения заключается в том, как выбрать оптимальный набор весов $\lambda$ для нашей формулы классификации?

Существует несколько способов получения оптимального набора параметров. Один из них – максимизация функции правдоподобия. Для заданного набора параметров модели – это произведение вероятностей всех документов по их классам.

$$\log P(C|D,\lambda) =\sum_{(c,d)\in(C,D)}\log P(c|d,\lambda) =\sum_{(c,d)\in(C,D)}\log\frac {\exp\sum_i^{n \times k}{\lambda_i}f_i\left(c,d\right )} {\sum_{\tilde{c}\in C}{\exp\sum_i^{n \times k}{\lambda_i}f_i\left(\tilde{c},d\right )}}$$

Функция условного правдоподобия maxent-классификатора над корпусом документов $(C,D)$

Набор параметров при котором достигается максимум значения этой функции и является оптимальным. Имеем типичную задачу численной оптимизации.

Обычно, для того, чтобы найти максимум функции, оперируют её градиентом. Если градиент известен, можно использовать различные алгоритмы для нахождения максимума, самый простой из которых градиентный спуск. Сам по себе, алгоритм градиентного спуска довольно прост. Он заключается в итеративном рассчете градиента функции в текущей точке и смещения в направлении градиента на некий шаг. Так до тех пор, пока не будет достигнута цель оптимизации. Полное описание этого алгоритма выходит за пределы заметки.

Градиент – это вектор, указывающий направление в котором функция растет наиболее интенсивно.

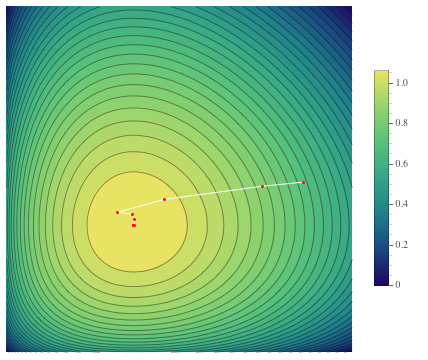
Визуализация произвольной функции методов градиентного спуска — Визуализация процесса оптимизации произвольной функции двух аргументов (показаны изолинии функции и апроксимационные шаги алгоритма)

Частные производные функции правдоподобия, которые составляют градиент, выглядят следующим образом:

$$ \frac{\partial\log P(C|D,\lambda)}{\partial\lambda_i}= \sum_{(c,d)\in(C,D)}{f_i(c,d)}- \sum_{d\in D}{\sum_{c\in C}{P(c|d,\lambda)f_i(c,d)}} $$

Частная производная функции условного правдоподобия

В этой формуле я хотел бы обратить ваше внимание на две группы, выделенные фигурными скобками. Первая – это количество срабатываний классификационного признака на обучающем корпусе (empirical count). Вторая – это предсказанное нашей моделью количество количество срабатываний классификационного признака на том же корпусе (predicted count).

В точке экстремума все частные производные, а следственно и градиент, равны нулю. Таким образом, вся эта нетривиальная математика приводит нас к очень простому выводу: оптимальная модель – это модель, предсказания которой совпадают с эмпирическим количеством срабатываний классификационных признаков в обучающем корпусе документов.

В заключение, несколько фактов относительно функции правдоподобия, её градиента и процесса оптимизации:

оптимальное распределение и максимум функции правдоподобия гарантированно существуют;
у функции правдоподобия один глобальным максимум;
найденные данным методом параметры описывают распределение с максимальной возможной энтропией.

Пример использования OpenNLP Maxent Link to heading

Корректная реализация собственного классификатора максимальной энтропии требует определенного опыта в области машинного обучения. Поэтому, если вам надо получить конкретные результаты, то лучше воспользоваться готовыми решениями. Для Java, есть два проекта, которые предлагают готовый инструмент: классификатор максимальной энтропии из состава проекта OpenNLP и логистическая регрессия в Apache Mahout. Здесь я опишу, как использовать OpenNLP. Исходный код примера доступен на github.

Проще всего будет тем, кто использует Maven для управления зависимостями. Достаточно прописать следующую зависимость в проекте:

<dependency>
  <groupId>org.apache.opennlp</groupId>
  <artifactId>opennlp-maxent</artifactId>
  <version>3.0.2-incubating</version>
</dependency>

Затем, необходимо реализовать класс, который будет извлекать из текста классификационные признаки в формате OpenNLP. Для этого необходимо реализовать интерфейс EventStream. Этот интерфейс представляет собой итератор по объектам типа Event. Каждый Event является обучающим семплом, который содержит в себе массив классификационных признаков и результирующий класс (context и outcome в терминологии OpenNLP). Классификационный признак – это просто напросто уникальная строка.

Обучение запускается методом GIS.trainModel(), который принимает на вход итератор по Event‘ам, а также некоторые параметры процесса обучения, из которых стоит отметить следующие:

iterations — лимит количества итераций процесса обучения;
cutoff – минимальное количество срабатываний классификационного признака, при котором признак допускается к обучению. Признаки с частотностью меньше cutoff, игнорируются;
smoothing— булевый флаг включающий сглаживание. Сглаживание в алгоритмах машинного обучения тема отдельная. Вкратце, сглаживание может дать более качественную модель, но за счет более сложного процесса обучения. До тех пор, пока у вас есть техническая возможность лучше его использовать.

Результирующую модель можно сохранить в файл при помощи следующего кода:

SuffixSensitiveGISModelWriter writer = new SuffixSensitiveGISModelWriter(model, new File("maxent.model"));
writer.persist();

а прочитать из файла при помощи следующего:

SuffixSensitiveGISModelReader reader = new SuffixSensitiveGISModelReader(new File("maxent.model"));
reader.getModel();

Если у вас остались вопросы, оставляйте из в комментариях. Подписывайтесь на RSS для того чтобы получать обновления. Если вам понравилась эта заметка, плюсуйте или поделитесь ссылкой в социальных сетях.

Ссылки по теме Link to heading

Using Maximum Entropy for Text Classification — Kamal Nigam, John Lafferty, Andrew McCallum;
A comparison of algorithms for maximum entropy parameter estimation — Robert Malouf;
Maxent Models and Discriminative Estimation. Generative vs. Discriminative models — Christopher Manning